“¿Por qué, en tiempos de paz, los amigos pueden convertirse en enemigos? ¿Y por qué, en tiempos de guerra, los enemigos pueden convertirse en amigos?”

Ambos interrogantes son los que inspiran al juego disponible en ncase.me/trust (creada por Nicky Case) que ilustra las decisiones que pueden tomar distintos jugadores, en diferentes instancias, cuando buscan el mayor bienestar posible. Una hermosa y práctica manera de enseñar lo que es teoría de juegos, concepto ya abordado con el Guasón y Friends.

La aplicación ofrece distintos juegos y también una explicación teórica sobre cada uno de ellos. En las líneas que siguen solo se explicará lo básico de la plataforma con el fin de sentar la forma con la que se deben pensar  estos tipos de desafíos.

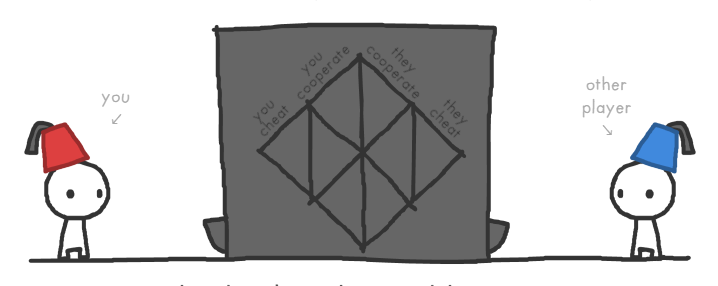
En todos los niveles tenemos la misma escena. Dos jugadores están separados por una máquina. Cada uno de ellos tiene una moneda y deben decidir si insertarla en la máquina o no. En un principio, nosotros somos uno de esos individuos. Si insertamos la moneda, la otra persona recibe 3 de ellas. Si no la insertamos, nosotros nos quedamos con esa moneda y la otra persona no recibe nada. Esto mismo vale para el otro jugador. Las opciones para ambos son, entonces, poner una moneda (colaborar – “C”) o no (no colaborar – “NC”). 

Pensemos. Tenemos dos opciones, y la otra persona también. Tenemos que encontrar cuál es nuestra mejor estrategia disponible. Para ello, es útil pensar qué nos conviene hacer para cada estrategia del otro. 

Si el otro elige C, ¿qué hacemos?. Si optamos por C, ambos entregamos una moneda y recibimos tres a cambio, por lo que el resultado neto para nosotros es +2. Si optamos por NC, nosotros ganamos 3 monedas y la otra persona pierde una. En resumen, si la otra persona coopera, a nosotros nos conviene no cooperar, dado que en el primer escenario (C) obtenemos +2 y en el segundo (NC) +3.

Si el otro elige NC, ¿qué nos conviene? Si optamos por NC, ninguno pierde pero tampoco gana nada (0 para ambos). Si cooperamos, nosotros perdemos una moneda (-1). En resumen, si la otra persona no coopera (NC), a nosotros nos conviene no cooperar (NC). Ups. ¿Qué nos dice el análisis?

(Si el otro elige C, me conviene NC. Si el otro elige NC, me conviene NC).

Que no importa qué elija el otro, lo mejor que podemos hacer es no cooperar. ¿Y qué sucede? Si el otro hace el mismo análisis racional, también va a elegir no cooperar.

Resultado: ambos nos quedamos con cero. A pesar de la nula ganancia, ambos estamos conformes con nuestra decisión dada la decisión del otro. Estamos en el famoso equilibrio de nash, ninguno se arrepiente de su decisión. Ahora bien, no estamos en el mejor de los mundos posibles. Existe un “óptimo de Pareto“, en el cuál la situación de uno de los dos, y en este caso la de ambos, puede mejorar sin que empeore la del otro. Es decir, ¡a los dos jugadores les conviene cooperar! Así tendrían ambos +2.

Este análisis (también disponible en la aplicación) corresponde al modelo de juego en el cuál se juega una sola vez. ¿Qué sucede si jugamos más de una vez? ¿Se puede llegar al óptimo de Pareto?

Tal vez podamos elegir cooperar para transmitirle al otro un mensaje: “cooperemos, elijamos C”. 

Sin embargo, siempre está la tentación de no cooperar, puesto que se obtienen más monedas. Pero esto tiene un precio: probablemente la traición consiga que de ahora en más el engañado siempre elija no cooperar, y desde allí lo único que se van a poder obtener en cada ronda son cero monedas. Es decir, si venimos cooperando y ganando dos monedas cada uno: ¿vale la pena elegir no cooperar para obtener una moneda más a costa de que en las próximas rondas elijamos el equilibrio de nash que no es pareto óptimo?

En pocas palabras, lo que la teoría indica, es que la traición va a ser más factible cuanto más corto sea el juego y cuanto mayor sea la recompensa que obtenemos de ella. Por otra parte, cuánto más valor se le de al corto plazo mayor va a ser la probabilidad de no cooperar, puesto que vamos a valor mucho más las monedas hoy que las que podamos conseguir mañana.

Alguien podría decir que la teoría estaría suponiendo que solo hay un tipo de jugador: el racional. Pues no, también se le pueden agregar distintos tipos de estrategas, como los que siempre cooperan, no importa qué, o los que, al contrario, siempre eligen no hacerlo. También están los que dejan sus decisiones libradas al azar (el 50% de las veces cooperan y el otro 50% no), entre otros.

¿Están estos personajes en el juego? Claro que sí. Para descubrirlos, estudiarlos y entenderlos, solo resta entrar al sitio.